在web页面中展示图片或者其他平面图形是很容易的。但是当涉及到展示3D图形时就显得不是那么的容易了,因为3D几何体比2D的更为复杂。要做到这一点的话,你可以使用专门的技术和库比如webGL和three.js来实现。
当然,如果你只是想显示一些基本的形状(比如立方体),这些技术并不是必须的。并且,这些技术和库并不能帮助你理解它们是如何生效的以及我们应该怎样在屏幕上绘制3D形状。
本教程的目的是教我们在web中并且不使用webGL技术应该如何够制作一个简单的3D引擎。首先,我们看看如何来存储3D形状,然后,我们分别在两种视图中如何来显示这些形状。
存储和改变3D图形
所有的形状都是多面体
虚拟世界与现实世界主要的不同之处在于: 没有什么是连续的,一切都是离散的。例如,你不能在屏幕上绘制一个完美的圆,你可以画一个有很多条边的正多边形去无限接近一个圆,正多边形的边越多,则你想要画的那个圆就越完美。
[TODO]
In 3D, it’s the same thing and every shape must be approached with the 3D equivalent of a polygon: a polyhedron (a 3D shape in which we only find flat faces ant not curved sides as in a sphere). It’s not surprising when we talk about a shape that is already a polyhedron, like a cube, but it’s something to keep in mind when we want to display other shapes, like a sphere.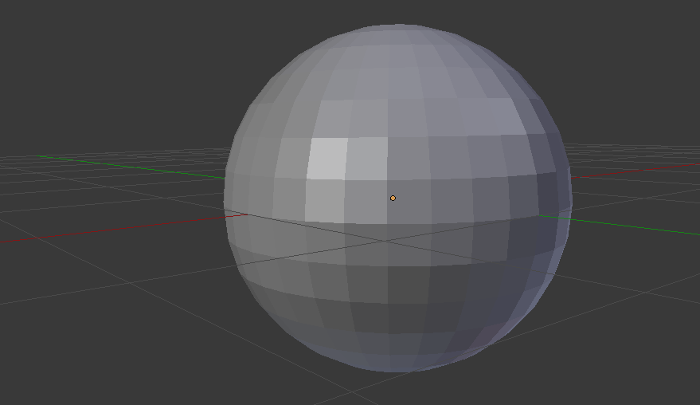
存储一个多面体
想要存储一个多面体, 还记得在数学中我们是怎样来标示的。我们在学校学过一些基本的几何图形,为了表示一个正方形,我们把它叫做ABCD ,使用A,B,C,D来表示四个顶点以构成一个正方形。
对于我们的3D引擎也是一样的,我们将首先存储形状的每个顶点,然后这个形状将列出它的每个面,并且每个面将列出其顶点。
我们需要有一个合适的结构来表示一个顶点,在这里,我们创建了一个类来保存顶点坐标。
1 | var Vertex = function(x, y, z) { |
现在,我们可以使用任何一个对象来表示一个顶点了,就像下面这样:
1 | var A = new Vertex(10, 20, 0.5); |
接下来,创建一个class来表示多面体.以立方体为例.
1 | var Cube = function(center, size) { |
使用上面创建的Cube类,我们可以通过指定中心点(center)和边缘长度(size)的方式来创建一个虚拟的立方体。
1 | var cube = new Cube(new Vertex(0, 0, 0), 200); |
Cube类的构造函数通过生成立方体的顶点来确定一个立方体,这些顶点的位置是通过指定中心点位置与立方体大小计算出来的。下面的图示表示得很清楚,我们在下图可以看到这8个顶点的位置。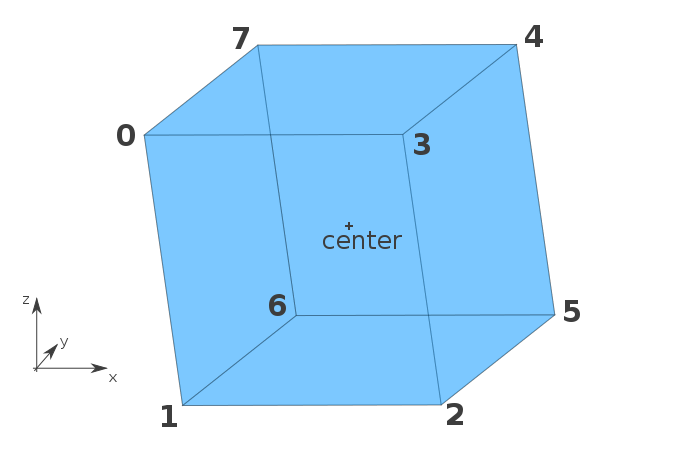
接着,列出每个面。每个面都是一个正方形,因此需要指定四个顶点。在上面的代码中我通过一个数组来表示一个面,如果你有需要的话,你可以创建一个专门的class来表示。
创建一个面需要四个顶点,但是我们不需要重复的指定它们的位置,它们都保存在 this.vertices[i] 这个对象中,这是非常有用的,但还有另一个原因。
通常地,JavaScript尝试使用尽可能少的内存。为了实现这个目标,通过函数参数传递对象的时候,这个对象是不会被拷贝或者被存为数组的。对于我们使用的情况,这是一种极好的行为。
事实上,每一个顶点包含了三个数字(坐标),必要的话我们可以再增加几个方法(method)。如果每个面我们都保存一份copy的顶点值,这样会浪费很多内存。在这里,我们都是使用引用的方式: 每个坐标(以及其他方法)都只存储一次,每个顶点被三个不同的面使用,只需要存储这个顶点的引用而不是把这个顶点都copy出来存储,这样仅仅使用了原来内存的1/3(或者更少)就够了。
需要三角形吗?
如果之前使用过3D技术(比如Blender,webGL等),你可能觉得我们应该使用三角形。但是呢在这篇文章中没有选择使用三角形(注: 确定一个面只需要三个点就可以了)。
为什么没有选择使用三角形呢,因为这是一篇以介绍为主的文章,在文章中展现的基本形状是立方体。在我们的例子中,使用三角形来显示正方形比其他任何事情都复杂。
但是如果你想要构建一个更加完整的渲染,你需要知道三角形才是首选,主要原因有两个:
- 纹理: 由于一些数学上的原因,在面(faces)上面显示图像(images)需要使用三角形.
- 一些奇怪的面: 三个顶点总是在同一个平面上的,然而你也可以添加第四个点,这个点可能就不在那个平面上了,你可以再创建一个面连接这四个点。 在这样的情况下,我们别无选择,只能分割出来两个三角形(就像对折一张纸一样)。但是如果使用三角形的话,你可以很随意的控制和选择从哪里开始分割。
让多面体动起来
还有一个存储顶点引用而不是存顶点副本的优势是,假如要修改这个多面体的时候,还能将本来的三个操作简化为了一个操作。(注: 比如保存了三个相同的顶点,如果对这个顶点进行移动,那么需要对这三个点都进行操作才正确,而如果使用引用的方式的话,只需要移动一个点就可以了。)
为什么呢? 来回顾一下数学课上学的东西.当想要平移一个正方形的时候,实际上你不需要真正的去平移这个正方形,你只需要平移正方形的四个顶点就可以了。
在这里,也是相同的做法:我们不会去触碰正方体的那些面,而是只需要把想要的操作应用到每个顶点上就可以了。那些面的坐标都是使用引用的方式创建的,只要坐标改变了,那么对应的面也会改变。下面这个实例将展示如何平移创建好的立方体:1
2
3
4
5for (var i = 0; i < 8; ++i) {
cube.vertices[i].x += 50;
cube.vertices[i].y += 20;
cube.vertices[i].z += 15;
}
渲染图像
我们现在知道了如何存储一个3D对象并且知道了如何对它们进行移动。是时候该看见它们了!但是,为了更能明白我们需要做什么,还需要一小点背景知识。
投影
目前,已经能够存储3D坐标了。但是,一个屏幕只能展现二维坐标,因此需要有一种方法将3D坐标转化为2D坐标: 这在数学上我们称之为投影(projection)。3D到2D的投影是一个抽象操作,是通过一个叫做虚拟摄像机的东西来完成的。这个相机将3D对象坐标转换为2D的,然后把它们发送到屏幕上面渲染出来。我们假设这个相机在我们3D空间中的原点上面(坐标是(0,0,0)).
在本文的开头我们讨论过坐标使用x,y,z三个数字来表示。但是要定义一个坐标的话我们需要一个基准: z是不是纵坐标?是向下还是向上?我们并没有一个统一的答案,也没有约定,你可以随意的选择定义。你唯一需要记住的是当你改变3D对象的时候所遵循的规则必须是一致的,公式也会随坐标系不同而改变。在此文中,我选择的基准是: x轴从左往右,y轴从后往前,z轴从下到上。
现在已经明确该做什么了:使用(x, y, z)表示坐标,为了在屏幕上显示他们,我们需要将它转换成(x, z)的形式。因为屏幕是一个平面,为来能够显示出3D效果。
这里不仅仅只存在一个投影,更糟糕的是存在无限多不同的投影。在此文中我们可以看到两种不同类型的投影,这两种也是在实践中是最常使用的。
如何绘制场景
在展现图形之前,先写一个函数专门用来绘制。这个函数接收一个对象数组(数组中每个对象是一个Cube实例),第二个参数是canvas的contex对象,其它参数用来让图形被绘制在一个正确的位置上。
这个对象数组包含多个要被渲染的对象。这些对象必须遵循一点:都有一个faces属性,这个faces属性是个数组,用来表示这个对象的所有面。这些面可以是任何图形(正方形,三角形,甚至是十二边形),他们是由顶点组成的数组。
上代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26function render(objects, ctx, dx, dy) {
// 循环每一个多面体对象。
for (var i = 0, n_obj = objects.length; i< n_obj; ++i) {
//循环每个面
for (var j = 0, n_faces = objects[i].faces.length; j<n_faces; ++j) {
//当前面
var face = objects[i].faces[j];
// 绘制第一个顶点
var P = project(face[0]);
ctx.beginPath();
ctx.moveTo(P.x + dx, -P.x + dy);
//绘制其他顶点
for (var k = 1, n_vertices = face.length; k<n_vertices; ++k) {
P = project(face[k]);
ctx.linTo(P.x + dx, -P.y + dy);
}
// 关闭路径和面
ctx.closePath();
ctx.stroke();
ctx.fill();
}
}
}
需要对这个函数说明一下,更确切的说是说明这个project()是什么,那些个dx, dy又是什么。其余的基本没什么,就是循环每个对象然后画出每个面。
顾名思义,project()函数就是用来将3D坐标转换成2D坐标的投影。它接收一个3D空间顶点,然后返回一个在2D平面上的点。2D平面上的点我们这样定义:1
2
3
4var Vertex2D = function(x, y) {
this.x = parseFloat(x);
this.y = parseFloat(y);
}
为了保持传统写法,我将坐标(x, z)重命名了(x, y), (之前定义的3D坐标系统中z轴是纵轴, 而2D坐标中y轴是纵轴)这仅仅是写法问题。如果你想要使用z的话也是可以的。
具体的project()函数的实现你将会在下一节中看到, 它取决于你选择的投影类型。但是不管是什么类型,而之前编写的render()函数是不会改变的。
坐标一旦在平面上了,我们就可以把它们绘制在canvas上面,这就是我们想做的。这里有一个小技巧是我们不会真正的绘制由project()函数返回回来的坐标点。
实际上project()函数返回的是一个虚拟2D平面上的点,它的原点和定义的3D空间中的原点是一样的。但是我想要原点在canvas画布的正中心位置上,那就是为什么要平移坐标了。顶点(0, 0)不在canvas画布的中心,但是(0+dx, 0+dy)在。因此只需要将dx=canvas.width/2,dy=canvas.height/2就可以了。
最后,最后一个细节是:为什么我们使用-y而不是直接的使用y? 原因在于我们选择的基准是: z轴是从下到上的,在我们的场景中z坐标是向上为正的。但是在canvas中,y轴是向下的,y坐标越往下,值越大。这就是为什么我们要把y坐标取值为z的负值。
目前render()函数已经很明确了,现在来看看project()函数
正交视图
让我们从正交视图开始,这也是最简单的一种视图,他能很好的帮助我们理解。
有三个坐标值,但是我们只想要两个,在这种情况下最简单的做法是什么呢?那就移除一个坐标值,在正交投影中就是这样做的。让我们移除表示深度的坐标值y.就像下面这样:1
2
3function project(M) {
return new Vertex2D(M.x, M.z);
}
现在你可以测试我们文章中的所有代码了, it works!恭喜你,你已经能在屏幕中绘制一个3D图形了!
这里有个在线示例, 你可以使用鼠标交互来旋转立方体.
See the Pen 3D Orthographic View by SitePoint (@SitePoint) on CodePen.
有时候正视图就是我们想要的.因为它保留了相似性的优势。但是这不是最自然的视角, 我们的眼睛看物体并不是像那样的,这就是为什么我们会看到第二个投影: 透视图
透视
透视图要比正交投影稍微复杂一点,我们需要做一些计算,当然这些计算并不是那么复杂的,你只需要知道一点就够了: 如何使用截线定理
要理解为什么,下面用一个图示来表示正交投影,用正交的方式将我们的点投影到一个平面上。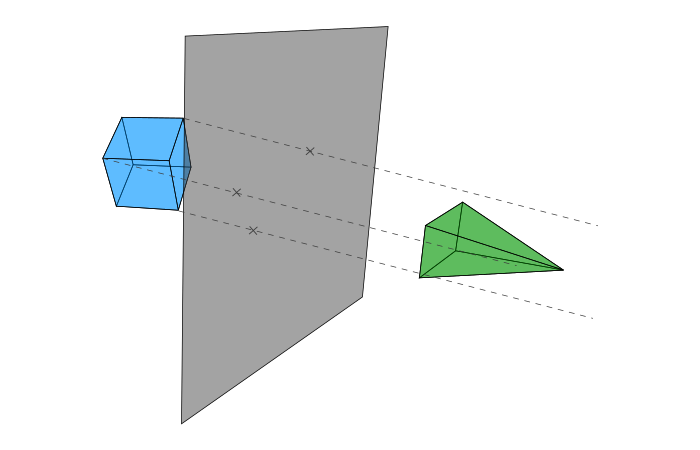
但是在现实生活中,我们的眼睛看物体更像下面这样: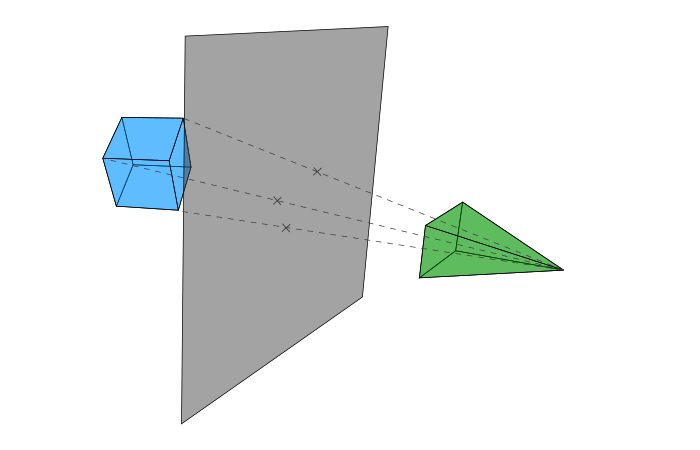
两个基本步骤
- 连接原来的顶点和相机的原点形成一条线.
- 投影就是这条线与平面的交点.
与正交投影相反的是, 定平面的位置是非常重要的:如果你这个平面放在远离相机很远的位置和你放在很近的位置所得到的效果是不同的。在这里我们把它放在离相机距离为d的位置.
在3D空间中,从顶点坐标M(x, y, z)开始,我们要计算在平面上的投影坐标M’(x’, y’);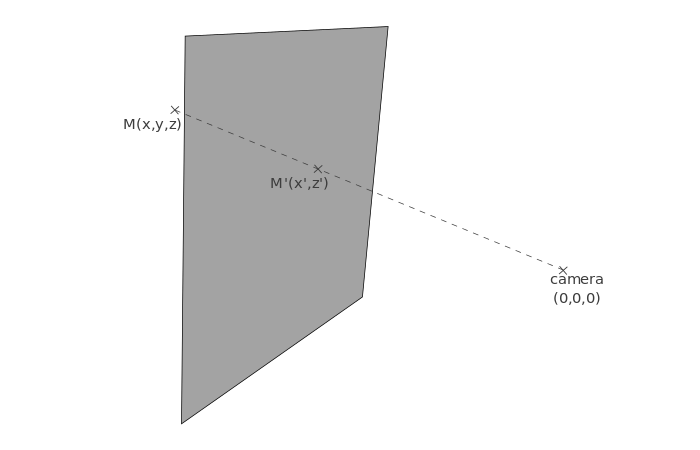
想一想应该如何计算这些坐标.让我们换一个角度来看,还是原来的图,但是现在从上面看。
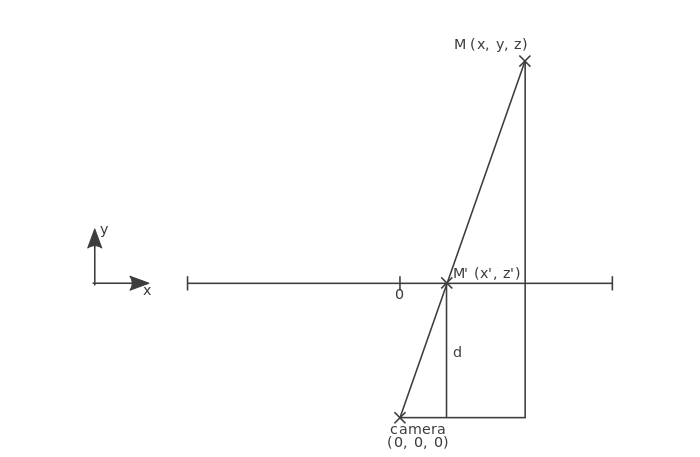
可以看到一个能使用截线定理的构造,在图示中,已经知道了一下值:x, y以及d. 想要计算x’,因此使用截线定理得:x’ = d / y * x.
现在如果你从一个侧面看同一个场景, 你会得到相似的图示.接着你可以得到z’的值.
z’ = d / y * z.
到这里就可以写出使用透视图的 project()函数了。代码如下:1
2
3
4
5
6
7function project(M) {
// 相机和平面的距离
var d = 200;
var r = d / M.y; // 注: 相似比
return new Vertex2D(r * M.x, r * M.z);
}
下面是在线示例:
See the Pen 3D Perspective View by SitePoint (@SitePoint) on CodePen.
结束语(不想译了….)
Our (very basic) 3D engine is now ready to display any 3D shape we want. There are some things you could do to enhance it. For example, we see every face of our shapes, even the ones at the back. To hide them, you could implement back-face culling.
Also, we didn’t talk about textures. Here, all our shapes share the same color. You can change that by, for example, adding a color property in your objects, to know how to draw them. You can even choose one color per face without changing a lot of things. You can also try to display images on the faces. However, it’s more difficult and detailing how to do such a thing would take a whole article.
Other things can be changed. We placed the camera at the origin of the space, but you can move it (a change of basis will be needed before projecting the vertices). Also, vertices placed behind the camera are here drawn, and that’s not a thing we want. A clipping plane can fix that (easy to understand, less easy to implement).
As you see, the 3D engine we built here is far to be complete, and it’s also my own interpretation. You can add your own touch with other classes: for example, Three.js uses a dedicated class to manage the camera and the projection. Also, we used basic math to store the coordinates, but if you want to create a more complex application and if you need, for instance, to rotate a lot of vertices during a frame, you won’t have a smooth experience. To optimize it, you will need some more complex math: homogeneous coordinates (projective geometry) and quaternions.
If you have ideas for your own improvements to the engine, or have built something cool based on this code, please let me know in the comments below!
英语渣作死第一次翻译…
原文地址:http://www.sitepoint.com/building-3d-engine-javascript/